Subset signatures¶
Sets (unary relations) can be introduced in a model through subset signatures. As we’ve already seen, unlike sub-signatures defined by extension, these are not guaranteed to be disjoint among themselves. In chapter Structural modeling we’ve seen the basic use of subset signatures, but since we actually expected those subset signatures to be disjoint, they were better modelled as extension signatures. That is not always the case, and in fact subset signatures can be used to encode powerful patterns, including something that resembles multiple inheritance.
Mixing subset and extension signatures¶
Suppose we wanted to add the ability to tag objects in a file system, for example as supported by operating systems like
macOS. The concept of tagged object is transversal to the signature
Object, since both regular files and directories can be tagged. On the
other hand, not all objects are necessarily tagged. So this feature is best
encoded as a subset signature as follows.
sig Tagged in Object {}
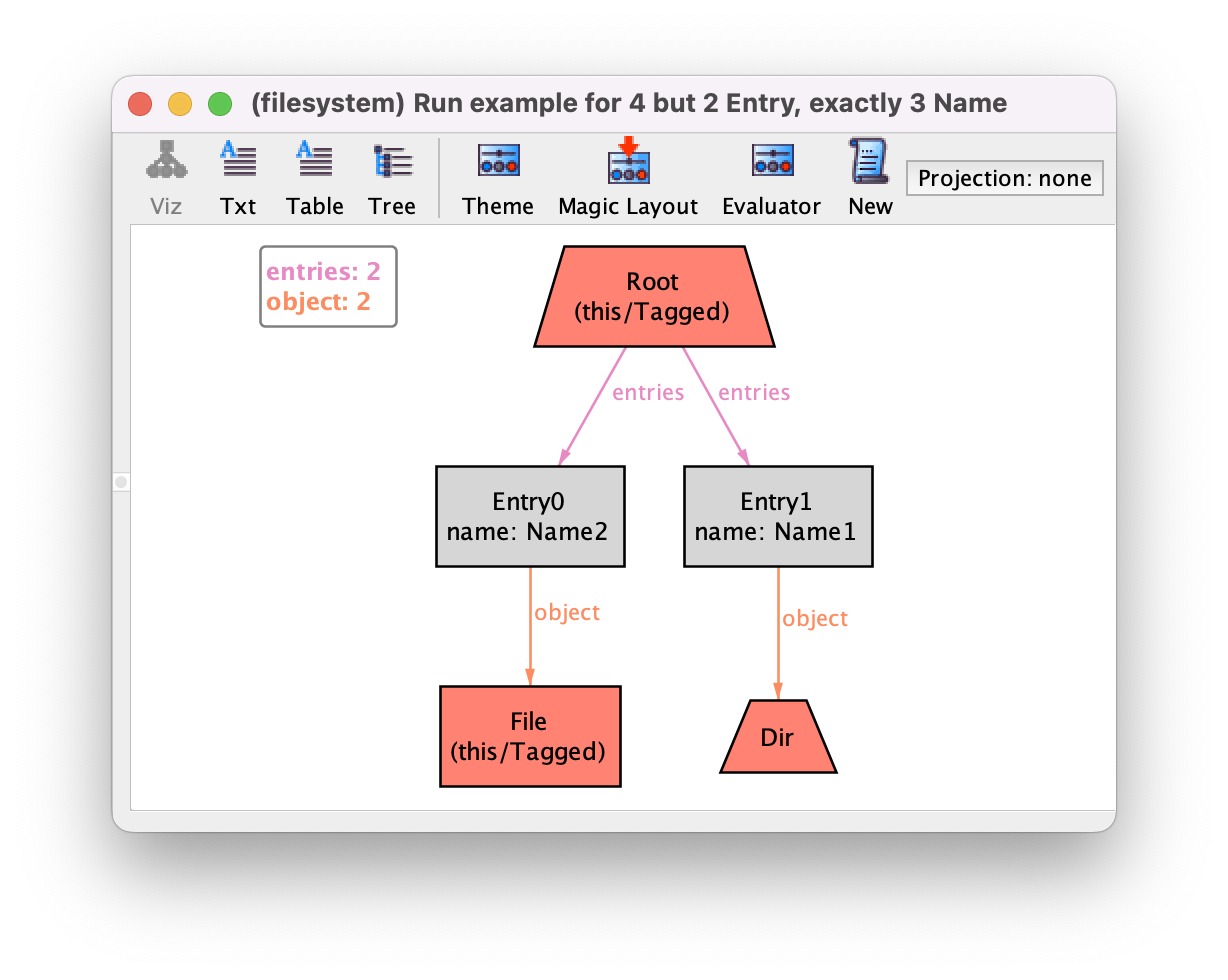
If we now ask the Analyzer for instances of this model there may exist objects
that are both in File and Tagged and Dir and
Tagged. The following is one such possible instance for the empty
command example. The fact
that an atom belongs to the Tagged subset signature is depicted with an attribute label below its name
(the name of the atom itself is based on the most specific extension signature to which it belongs).
Even more interesting, subset signatures can have their own fields declared
within. For instance, let’s introduce a signature Tag to represent
abstract tags, and then extend signature Tagged to also register the
non-empty set of tags assigned to each object, as follows.
sig Tag {}
sig Tagged in Object {
tags : some Tag
}
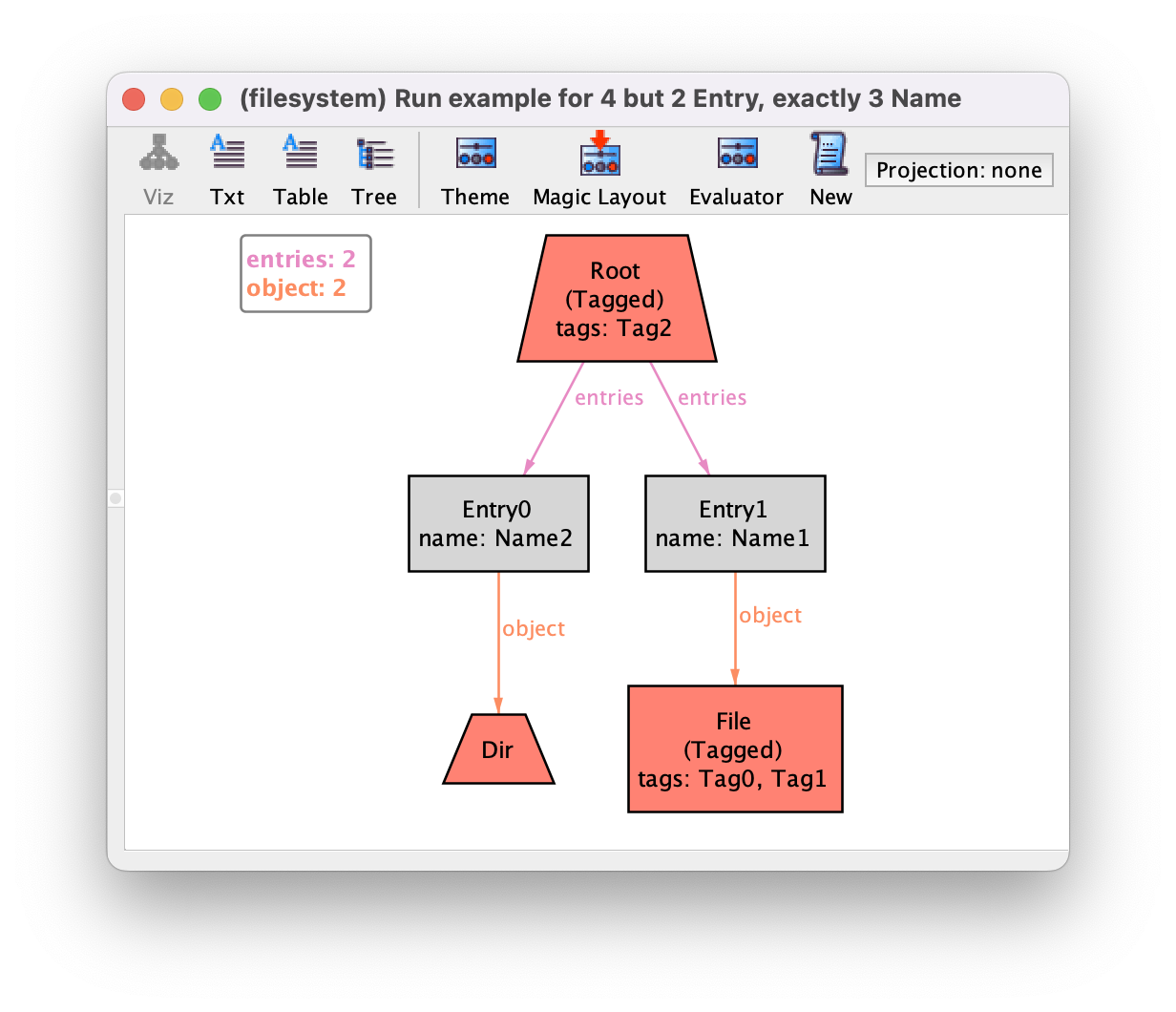
Now, for instance, any tagged directory will both be related through relations
entries (inherited from Dir) and tags (inherited from
Tagged). Below is one such example for the same command, where the root
has both entries and tags (in the theme, we’ve hidden Tag atoms, and set
field tags to be shown as an attribute).
Alloy model
Download and explore the files relevant for the model at this point of the book.
Simulating multiple inheritance¶
Suppose now we wanted to discriminate different kinds of tags, so that these can either be shapes (with a color) or labels (with a text message). This tag hierarchy could be declared as follows.
sig Color, Text {}
abstract sig Tag {}
sig Shape extends Tag {
color : one Color
}
sig Label extends Tag {
text : one Text
}
Suppose now we also wanted to add alerts that are tags that are both shapes and labels. In Alloy we don’t have multiple inheritance, so we cannot declare a signature Alert that both extends Shape and Label. Using subset signatures we could simulate multiple inheritance. The key idea would be to declare all three signatures as subsets of the Tag signature, and then use a fact to encode the type hierarchy constraints, namely the fact that Tag is abstract and that Alert is the set of tags that are both shapes and labels. We could do so as follows. Note that alerts would inherit both the color and text fields.
sig Tag {}
sig Color, Text {}
sig Shape in Tag {
color : one Color
}
sig Label in Tag {
text : one Text
}
sig Alert in Tag {}
One of the problems of this approach is that since the different kinds of tags are not proper extensions, their atom names will all begin with Tag, so to distinguish the different kinds of tags we would need to use the subset signature labels. Of course, we could also customize the theme to help us distinguish which tags fall in each category. In the following instance, we’ve
set the abstract top-level Tag signature to be white and have the default rectangle shape. Then, shapes are instead colored yellow, while labels are shaped as ellipses. As a consequence, alerts are yellow colored ellipses.
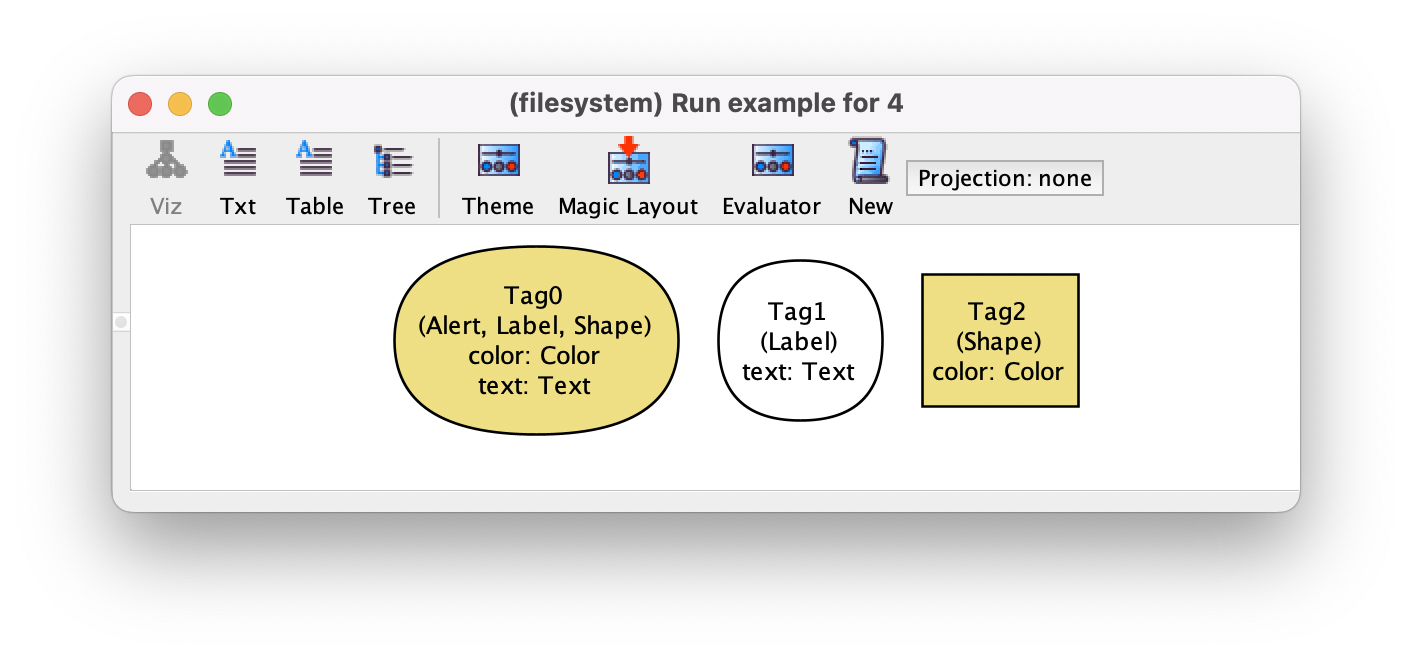
Alloy model
Download and explore the files relevant for the model at this point of the book.
Further reading
In this topic we’ve have used advanced theme customizations to ease the visualization of instances. Learn more about the Alloy Analyzer’s theme customization feature.
Cross-signature subsets¶
Another interesting feature of subset signatures is that they can be defined to
be a subset of a union of multiple signatures using the + operator,
rather than just one as we’ve seen thus far. Let us extend our example again,
and consider that our file system also supports symbolic links as a distinct
type of object.
sig Symlink extends Object {}
If we do not want symbolic links to be tagged, we could enforce this through an additional fact that
restricted the value of Tagged, but this can be directly achieved at the
signature level by adapting its declaration as follows.
sig Tagged in Dir + File {
tags : some Tag
}
Now subset signature Tagged is restricted to only Dir and File
atoms, excluding other kinds of objects. In this example Dir and
File share the same top-level signature Object, but signatures can
be defined as the subset of the union of completely unrelated signatures. To properly visualize instances, you will have to customize the theme again at this
point. This is because in the previous version, subset signature Tagged and field
tags were defined for the full signature Object in the theme; now, they are no longer defined for all objects, but only for signatures
File and Dir. At the theme customization pane, this will originate two duplicates of Tagged and tags, one for each of these two signatures, which
both have to be customized again.
One last, and less common, way to define subset signatures is through equality
rather than inclusion using the operator =. For instance, let’s say that
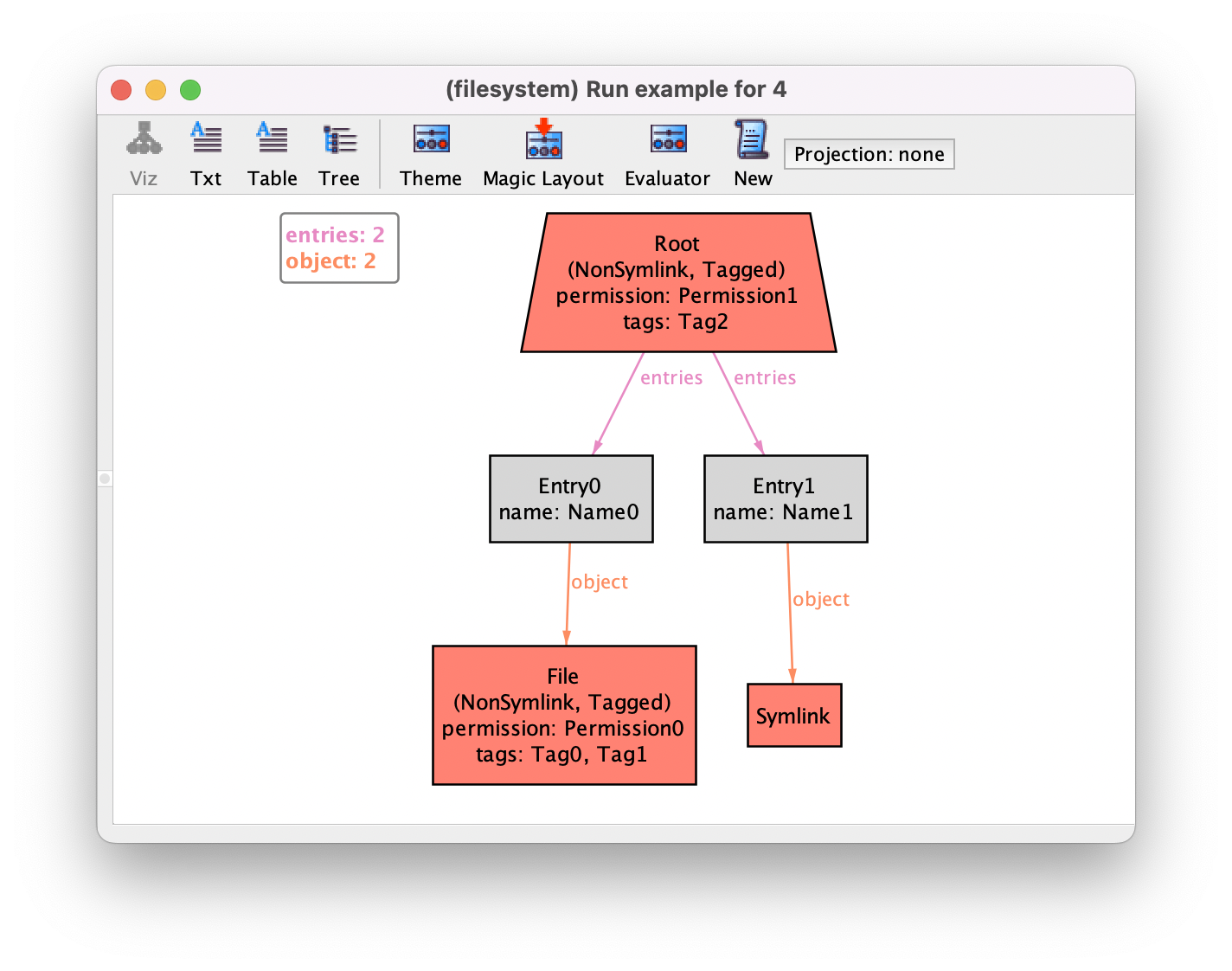
we wish to assign user permissions to all directories and files, but not to symbolic links. This could be done as follows.
sig Permission {}
sig NonSymlink = Dir + File {
permission : one Permission
}
An instance for the empty command for this version of the model is the following.
Obviously, this example is a bit contrived since a simpler solution would be to
extend Object with an abstract signature NonSymlink and then
have Dir and File extend that signature. However, we could also declare a subset that is equal to the union
of unrelated signatures, and that could not be declared in such a manner.
On a last note, due to all the flexibility of subset signatures, particularly the fact that they may contain atoms from unrelated signatures, they cannot be extended, only contain other subset signatures.
Alloy model
Download and explore the files relevant for the model at this point of the book.