The predefined ordering module¶
Alloy has some predefined modules in a special util namespace. One of them is util/ordering, a parametrized module that can be used to impose a total order in a signature.
In particular, this module defines a next relation that given an atom returns the next atom in the total order, and two derived singleton signatures first and last with the first and last atoms of the order, respectively. Note that last is the only atom without a next atom in the order. Module util/ordering also defines several derived predicates and functions to compare and compute the maximum or minimum of sets of elements (for example, gt is a predicate that can be used to compare if one atom is greater than another, and max is a function that computes the maximum of a given set of atoms).
Declaring totally ordered signatures¶
For example, let’s suppose we wanted to enrich our file system model with the creation timestamp of each entry. Since we will want to compare timestamps, we could first declare a totally ordered signature Time as follows.
open util/ordering[Time]
sig Time {}
The definition of signature Entry could now be changed to include the creation timestamp attribute.
sig Entry {
object : one Object,
name : one Name,
time : one Time
}
Of course, we should impose a new constraint stating that the creation timestamp of an entry should precede that of its children.
fact children_timestamp {
// The timestamp of an entry precedes that of its children
all e : Entry, t : e.object.entries.time | lt[e.time, t]
}
Note the use of a chain of compositions to get all timestamps of all entries contained in the object of an entry. If the object is a file this set will be obviously empty and the constraint holds trivially. If it is a directory, then the timestamp of the respective entry must be less than those of all its children.
If we run the example command with a scope of 3, and customize the theme to show timestamps as attributes, we could get the following example filesystem.
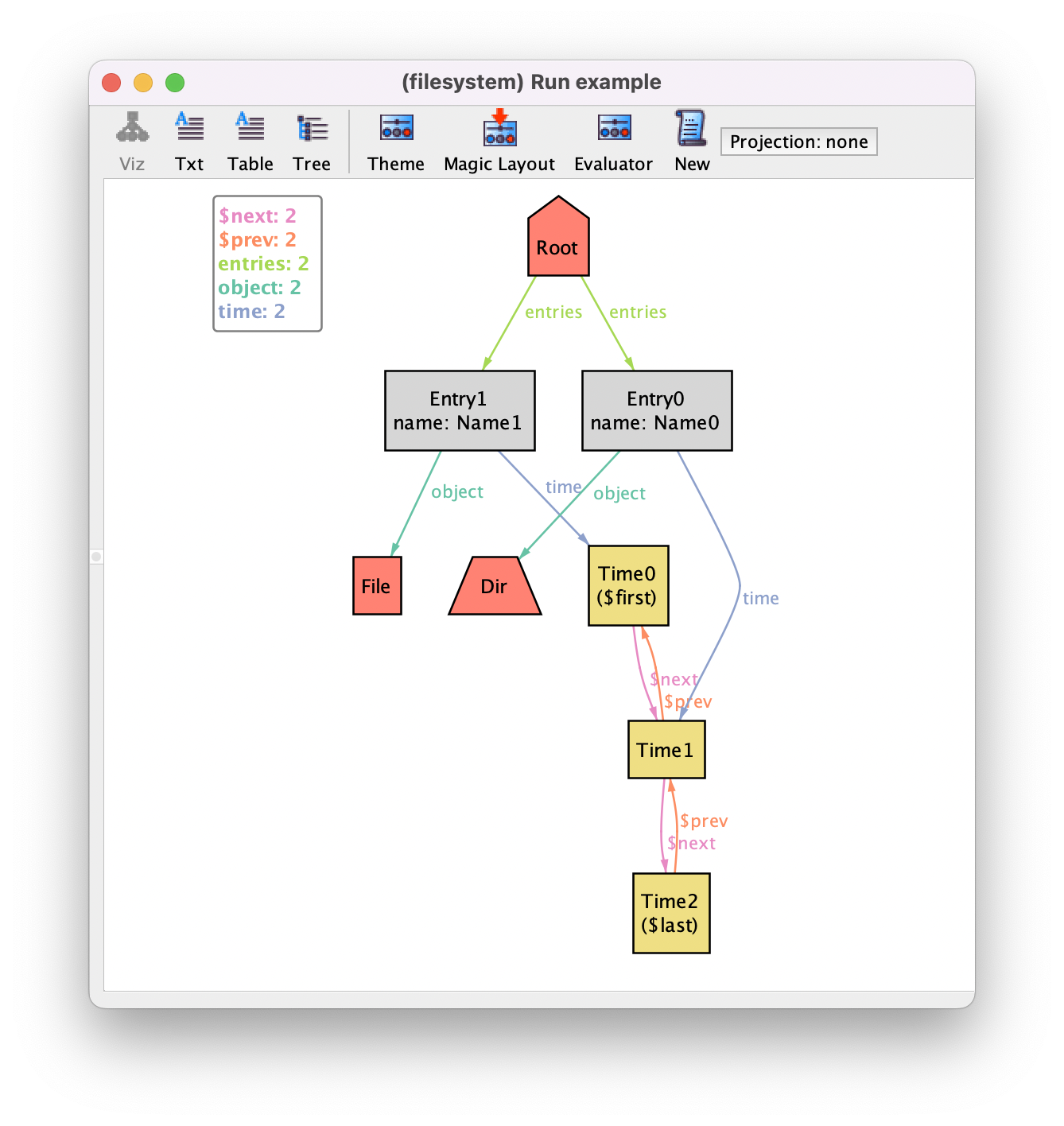
You can see in the visualization relations first, last, and next introduced by module util/ordering. If we are not interested in seeing these relations in the visualization, we can omit them.
In principle, this would make it very difficult to understand how the timestamps are ordered, and check if instances are valid.
However, the module util/ordering is handled in special way be the Alloy Analyzer, which will attempt to name the inhabitants of the ordered signature sequentially according to the order defined by next. So you can see in our instance that Time0 is the first, which is followed by Time1, and then by Time3, which is the last. If we really want to confirm the value of the next relation we could go to the evaluator and ask for its value. However, we will get an ambiguity error since next is also defined in the util/integer module that is imported by default. To disambiguate we could type the qualified name ordering/next instead.
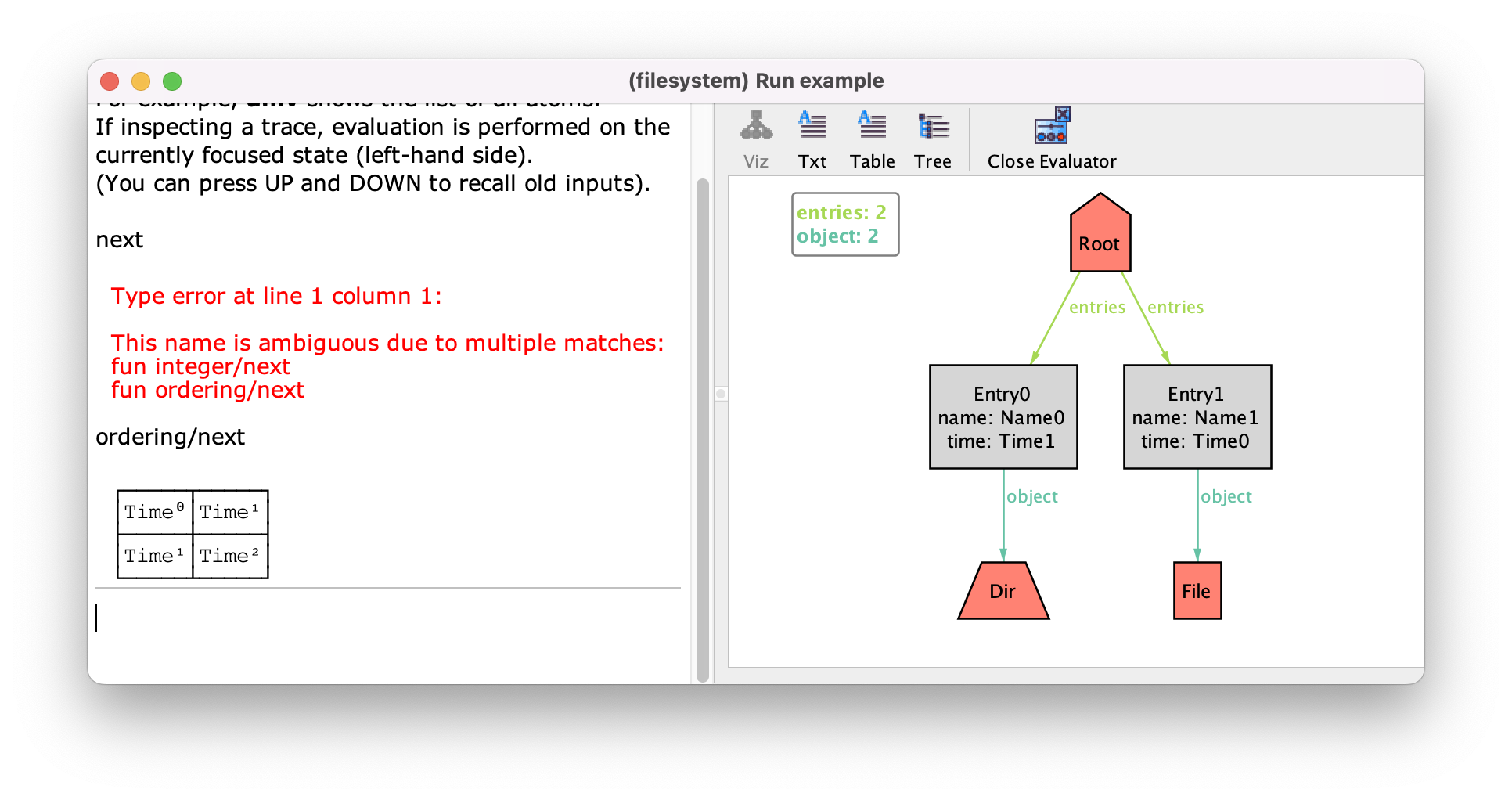
To see what other functions and derived relations are declared in util/ordering you can open it in the menu .
The above fact, imposing that the creation timestamp of an entry should precede that of its children, actually makes fact no_indirect_containment redundant, since it is no longer possible for directories to contain themselves directly or indirectly. We can confirm this by changing that fact to an assertion and using the Analyzer to verify it.
assert no_indirect_containment {
// Directories cannot contain themselves directly or indirectly
all d : Dir | d not in descendants[d]
}
check no_indirect_containment for 6
Analysis scopes¶
Besides naming the atoms according to the total order, module util/ordering has another peculiarity concerning the analysis. The scope of the signature that is passed as parameter to util/ordering is always exact even if not declared with exactly. The reason for this is to make analysis faster, but one should always be aware of this detail when running commands, as it can sometimes introduce inconsistencies, making run commands trivially unsatisfiable or check commands trivially valid.
As an example, consider the following (rather arbitrary) model of a finite sequence of natural numbers, distinguishing between even and odd numbers, and requiring the first in the sequence to be even and the last to be odd.
open util/ordering[Nat]
abstract sig Nat {}
sig Even, Odd extends Nat {}
fact {
all n : Even | n.next in Odd
all n : Odd | n.next in Even
first in Even
last in Odd
}
run example {}
If we execute the command example we get no instance! This is due to the fact that the default scope for Nat is 3, and since this signature is being totally ordered with util/ordering this scope is required to be exact. Unfortunately, with exactly 3 atoms in Nat it is impossible to satisfy the given constraints. If we change the scope of example to 4 then we will obtain one instance.
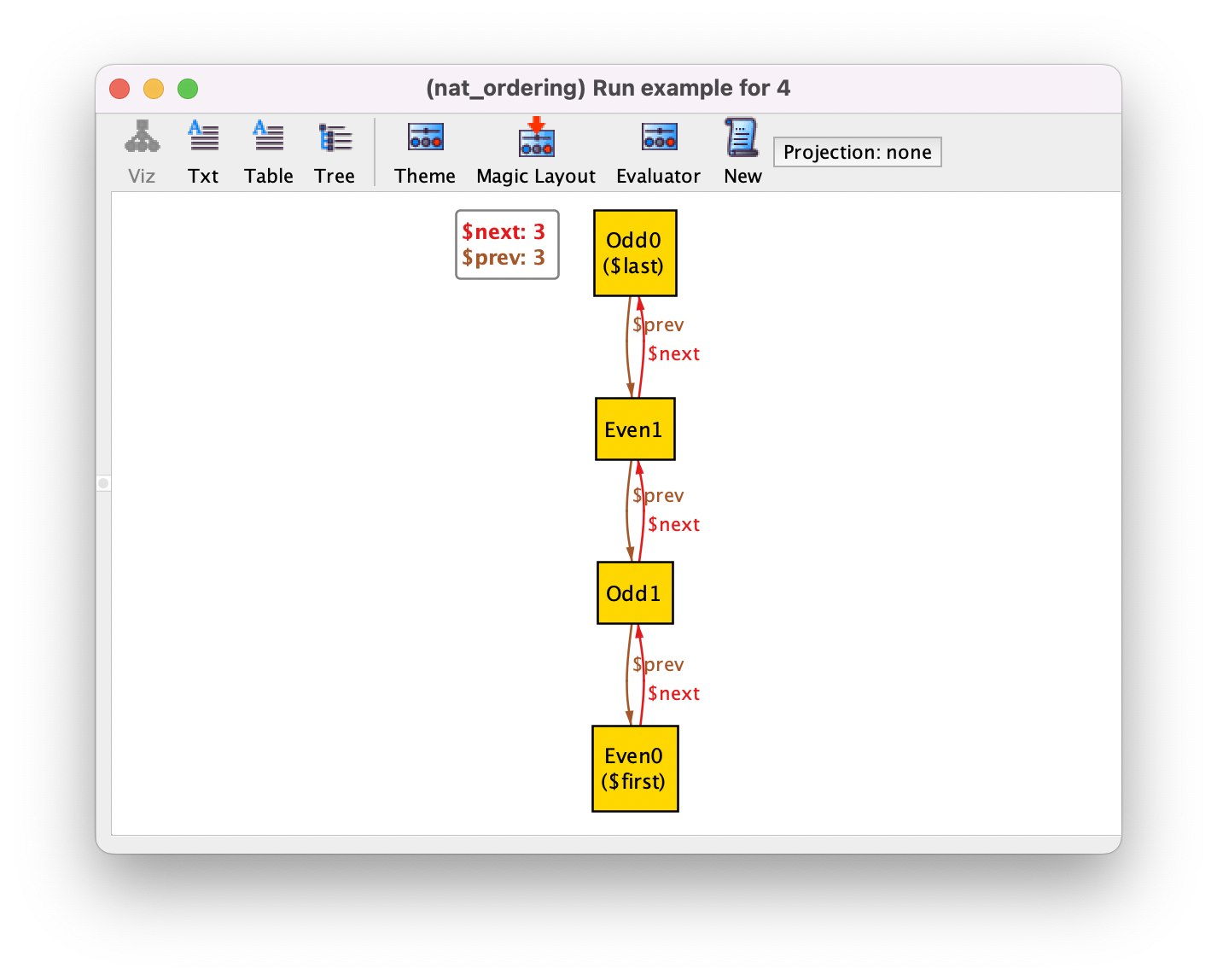
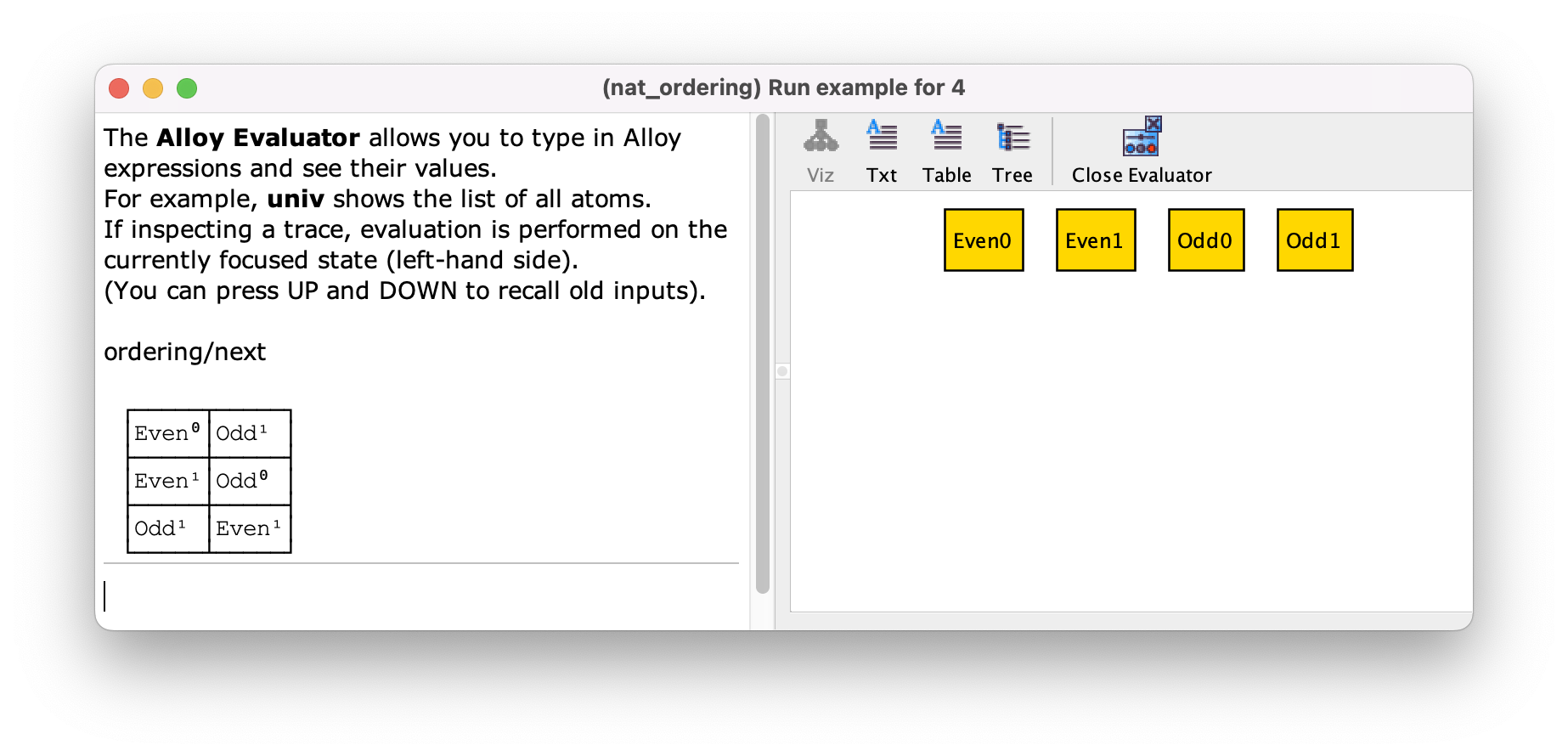
This is also an example where the naming of the atoms does not help in understanding what is the total order, since the ordered signature Nat is abstract and extended by Even and Odd. If you omit the util/ordering
relations from the visualization, you can always use the evaluator to consult the atom order.
As a last note on scopes, for efficiency reasons the util/ordering module also requires the parameter signature to be non-empty (it forces first and last to always contain exactly one atom), meaning that setting its scope to 0 will also result in an inconsistent specification.