Working with integers¶

Although using integers in Alloy may seem like a harmless decision, they have some particularities that may lead to unpredictable behaviour. Moreover, due to the nature of the procedures behind the Analyzer, using integers actually may have considerable impact in the performance. Integers should only be used if the specification actually requires arithmetic operations. For instance, identifiers may be encoded as integers in the system implementation for convenience, but will only need to be be tested for equality. Thus, during the system design such an identifier can actually be represented by an uninterpreted atom. If we additionally need to, for instance, compare identifiers, this can be achieved by imposing a total order on the atoms of the signature. Nonetheless, there are of course situations where we actually need to perform arithmetic operations over integers. This chapter shows how this can be achieved in Alloy, and which pitfalls to be aware of.

Models with integers¶

Integers are actually always enabled in every Alloy specification. For instance, if you execute any run command with a default scope, and use the Analyzer’s evaluator to check the value of expression Int you will get the following set.

-1

-2

-3

-4

-5

-6

-7

-8

0

1

2

3

4

5

6

7

Int is the built-in signature containing all integer atoms. You can also see that they always integrate the universe of discourse by evaluating univ. You’ll also notice that these integers are finite and that they are the 4-bit signed integers under Two’s-complement binary representation. Being aware of these three points - integers are atoms, bounded, and interpreted in binary - is essential to use integers in Alloy soundly.

Signature Int can be used as any other signature in the model, except that it cannot be extended (like all built-in signatures). Fields can have type Int, and signatures can be declared as subsets of Int. For instance, let us return to the file system example from chapter Structural modeling and try to extend our model with file sizes. In particular, we want to assign to each object an integer size, and also have a distinguished integer atom representing the maximum capacity of the system. This could be simply achieved as follows.

one sig Capacity in Int {}

abstract sig Object {
  size : one Int
}

After running the empty run command example, we could get an instance such as the following, after some theme customizations (by default, unconnected nodes of Int are set to hidden; we’ve turned this off, set all integer atoms to be hidden, but then only subset Capacity to be shown).

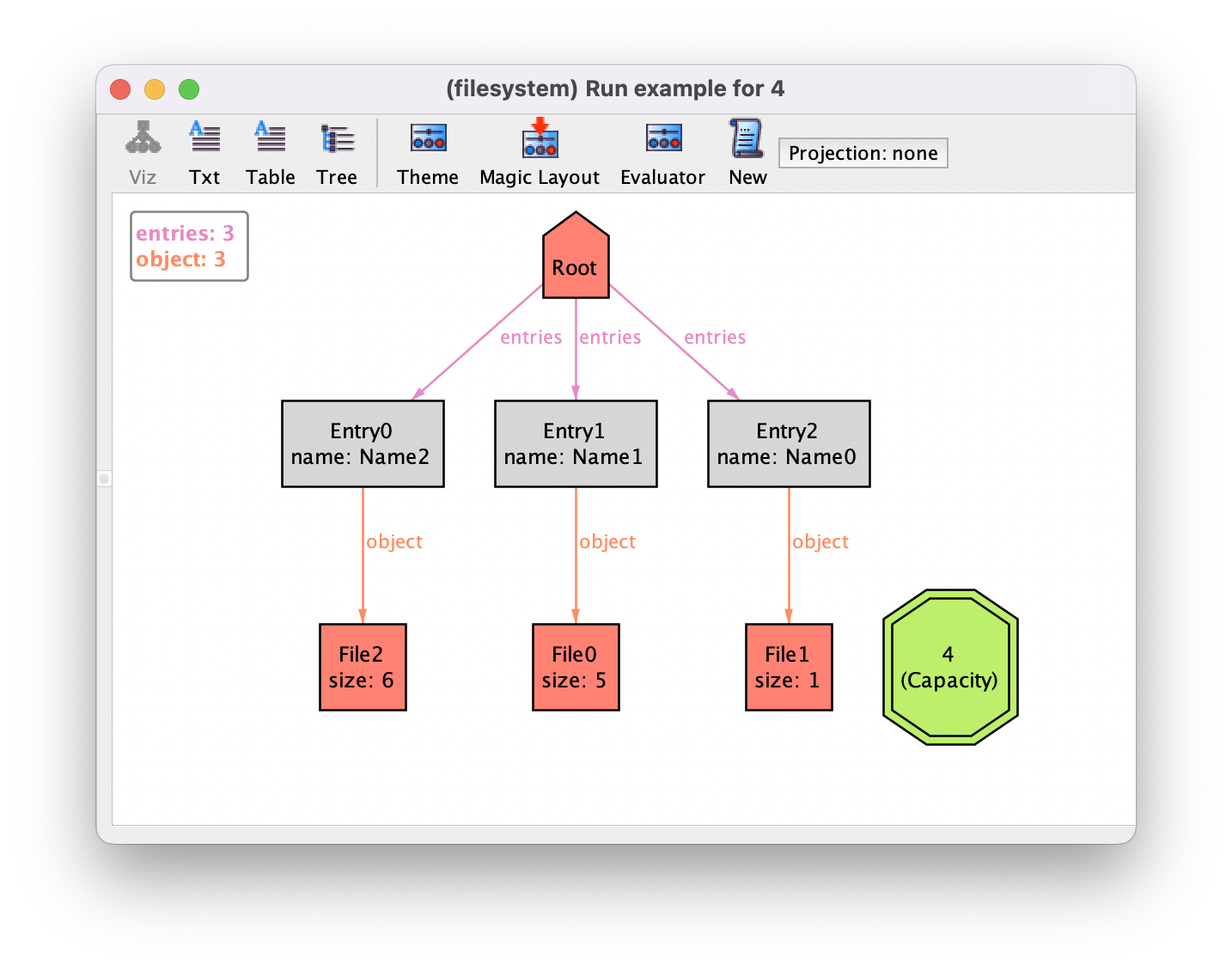
Alloy model

Full model for the section

Download and explore the files relevant for the model at this point of the book.

Integer operations¶

Let us the Analyzer’s evaluator to explore how to manipulate integers. Integer constants can occur in relational expressions (including in the model, unlike other atoms). Start by evaluating, for instance, 1+2. While initially surprising, getting the set of atoms {(1),(2)} was the only sensible solution: as everything Alloy, expressions 1 and 2 are actually singleton sets {(1)} and {(2)}, and + denotes the union of relations. For another sanity check, evaluate 1-1. This evaluates to the empty set {}, and not to the integer 0. Again, this is because - is the relation difference operator. Notice that, since these are valid relational expressions, no errors or warnings are thrown.

To perform arithmetic operations over integers, a special set of operators must be used. The table below presents the native integer operators supported by Alloy.

Operator	Description	Operator	Description
`fun/add`	Addition	`<<`	Left shift
`fun/sub`	Subtraction	`>>`	Right shift w/ zero extension
`fun/mul`	Multiplication	`>>>`	Right shift w/ sign extension
`fun/div`	Division	`>`	Greater than
`fun/rem`	Remainder	`<`	Less than
`fun/min`	Minimum integer	`>=`	Greater than or equal to
`fun/max`	Maximum integer	`<=`, `=<`	Less than or equal to
`fun/next`	Order relation	`sum`, `int`	Set to integer conversion

The negation of the comparison formulas can also be written by placing the negation operator next to the comparison operator (R not < S or R !< S for not (R < S), for example). The expressions that we evaluated above should actually be written as 1 fun/add 2 and 1 fun/sub 1. As expected, the result is again a singleton set that contain a single integer atom. By default, Alloy also imports a util/integer utility module that provides friendlier function and predicate versions of these operators. Some of those are listed below, but you can consult the full module through menu option File ‣ Open Sample Models….

Function	Description	Predicate	Description
`add[n1, n2 : Int]` `plus[n1, n2 : Int]`	Addition	`gt[n1, n2 : Int]`	Greater than
`sub[n1, n2 : Int]` `minus[n1, n2 : Int]`	Subtraction	`lt[n1, n2 : Int]`	Less than
`mul[ns : set Int]`	Multiplication	`gte[n1, n2 : Int]`	Greater than or equal to
`min[ns : set Int]`	Minimum of a set	`lte[n1, n2 : Int]`	Less than or equal to
`max[ns : set Int]`	Maximum of a set	`eq[n1, n2 : Int]`	Equal
`max`	Maximum integer	`pos[n : Int]`	Positive
`min`	Minimum integer	`neg[n : Int]`	Negative
`next`	Order relation	`nonpos[n : Int]`	Non-positive
`prev`	Reversed order relation	`nonneg[n : Int]`	Non-nositive

Since everything is a relation, integer operations actually apply to any set of atoms, even if it not singleton integer atom. This is something that is not used often, but since this throws no error, it is important to be aware of their semantics (arithmetic over non-unary relations always throws a type-error). Whenever an integer operation is applied to a set, the latter is implicitly cast into a single integer value, and the resulting integer wrapped back into a singleton set. The implicit conversion of set to an integer is done by applying the sum operator. If the relation is a singleton set, this will just result in the value of its atom, but if there are multiple integer values in the set, they will be summed together. So (1+2).plus[3] is actually (the singleton set) 6, and (1+1).plus[3] is still 4. Also, sum works on sets that contain atoms other than integer: they will just be ignored. If the set contains no integer atom (e.g., 3.plus[Root]), a type-error will effectively be thrown. This also highlights a difference between the relational = and the integer eq: while 1 = 1 + Root is false, 1.eq[1 + Root] is actually true.

Let us get back to the example and try to fix some of the issues evident in the instance above. For instance, we expect file sizes to be positive. This can be easily achieved with the following fact.

fact positive_sizes {
  // All file sizes are positive
  all f : File | gt[f.size, 0]
}

Another constraint that we would like to impose is that sum of the size of all files is less than the established capacity. However, using the operators we’ve seen so far, this is not possible to encode. At first sight, sum File.size could perhaps be used to sum the size of all files. However, if there are multiple files with the same size, that integer atom will only occur once in File.size and thus the sum will yield an incorrect value.

This can be addressed with another important integer operator, the sum quantifier (not to be confused with the sum unary operator). The sum quantifier iterates over a set of atoms and adds up the value of an integer expression over the quantified variable. Back to our example, the size of all files could be written as sum f : File | f.size, iterating over all files and summing their size. The following fact would enforce the desired constraint on capacity.

fact below_capactiy {
  // The sum of the size of all files cannot exceed the capacity
  (sum f : File | f.size) <= Capacity
}

One last, but still very useful integer operator, is the cardinality operator #, which calculates the number of atoms in a relation. For instance for a given directory d, expression #(d.entries) returns the number of entries of d. For instance, the following command will search for instances where the root has 3 objects.

run full_root {
  #(Root.entries) = 3
} for 4

Let us run this command and validate our model with the additional constraints. If you’re not aware of Alloy’s integer semantics, you may be surprised to find the following instance, where the sum of the size of the files clearly exceeds the capacity.

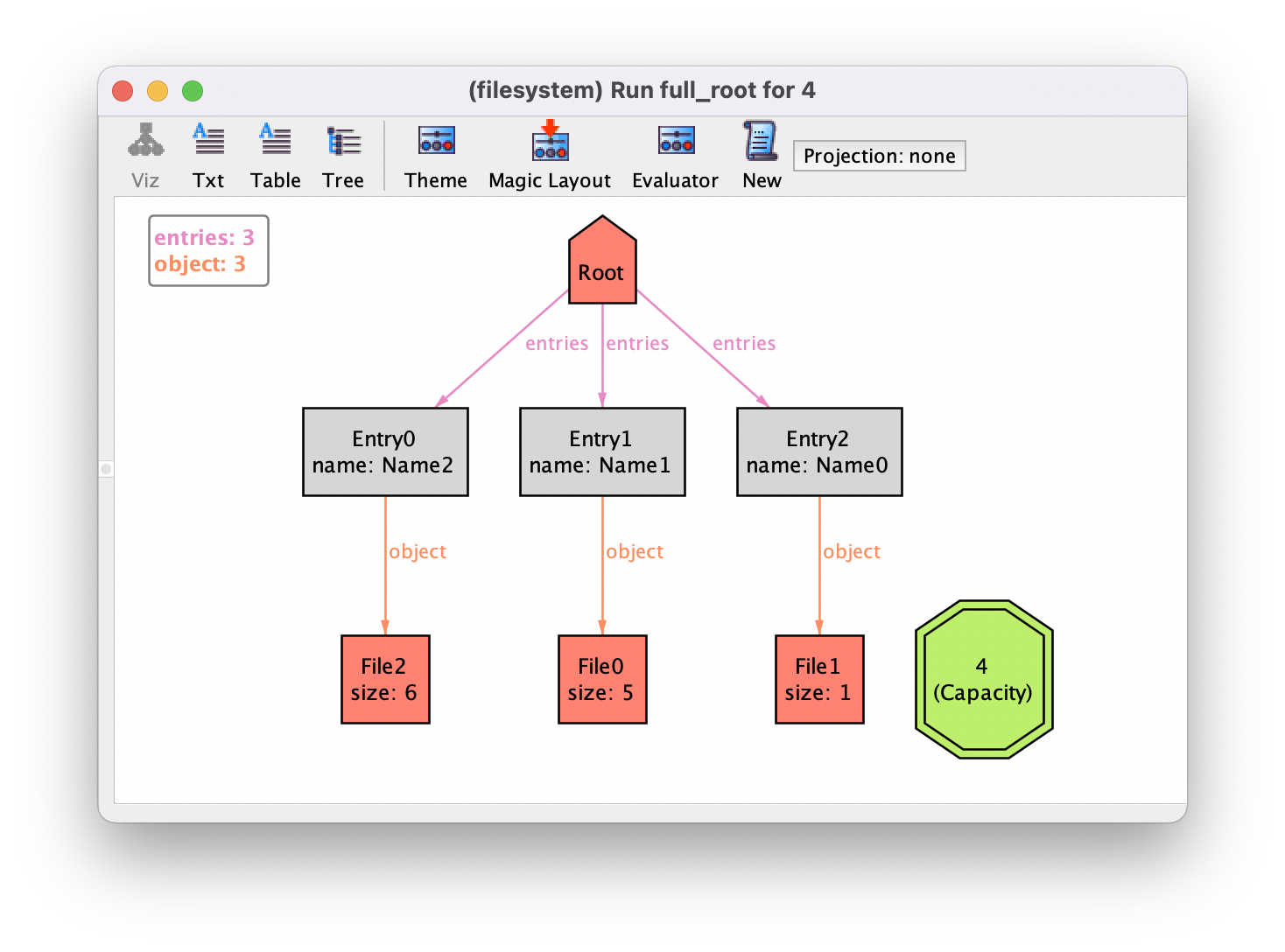
Alloy model

Full model for the section

Download and explore the files relevant for the model at this point of the book.

Dealing with integer overflows¶

Alloy implements a wrap-around semantics for integers, and given the limited number of available integer atoms, and the exhaustive nature of the Alloy analyses procedures, integer overflows are a common issue that must be addressed. With the default scope on integers they range from -8 to 7, so in the instance above 5.plus[1].plus[6] is effectively -4, which is smaller than the capacity 4 (you can test it in the evaluator).

The number of integer atoms available during analysis is defined by the scope on Int on the command declaration, as for other regular signatures. This scope does not set the number of integer atoms in the universe, but rather the size of their bitwise representation. This scope is 4 by default, which results in the 16 integers from -8 to 7. The scope for Int is always exactly defined as the integers available with the specified bitwidth (unlike the other signatures whose scope determines an upper-bound). Also, changing the overall scope of a command does not change the scope on Int: it must be explicitly set.

Nonetheless, our current model will exhibit overflows regardless of the scope for integers, because there are always instances where the size of the files will overflow. Although this may look cumbersome, overflows are a common issue in real systems, Alloy just happens to illustrate it in a smaller scale. So rather that completely forbid overflows, we should instead guarantee that our system model never reaches a state where such overflows occur. For instance, we can limit the size of objects with the following fact, that takes into consideration the maximum available integer and the number of objects in the universe.

fact size_limits {
  // Guarantee file sizes do not overflow
  all f : File | f.size <= div[max, #File]
}

Behind the curtain, the reason why integers behave like this in Alloy is because the Analyzer relies on SAT solvers for the analyses, which support only Boolean variables. Thus, integers are converted into bit strings during analysis, with a Boolean variable representing each bit, while integer operations are converted to their bitwise counter-parts. A side-effect of this is that large integer bitwidth scopes have a considerable toll on performance.

Alloy has the ability to ignore instances where any overflow occurs. This can be turned on in the menu option Options ‣ Prevent overflows. Any run command will no longer present instances with overflows, and these will also be ignored when running check commands. However, bear in mind that this will completely disregard instances where any overflow occurs, which may give a false sense of security. For instance, the obviously false check command below actually finds no counter-example when overflows are forbidden.

check big_files {
  all f : File | f.size > 10
}

This is because the constant 10 cannot be represented with the default bitwidth scope of 4 and overflows.

Alloy model

Full model for the section

Download and explore the files relevant for the model at this point of the book.