Inductive invariants¶
An invariant is a state property (that is, one that only depends on one state) that is true in every state of every trace. In terms of temporal logic, we can assert an invariant by putting the state property under an always connective, as was done for shared_are_accessible in the file sharing model.
assert shared_are_accessible {
always shared.Token in uploaded - trashed
}
Now suppose we want to check shared_are_accessible for an unbounded number of steps and an overall scope of 10.
check shared_are_accessible for 10 but 1.. steps
On a recent computer, this verification already takes a couple of minutes and this verification time would grow quickly if we increased the scope.
Is there an alternative, more efficient way to verify this invariant?
Verification by induction¶
Actually we could try to verify this property by induction, that is by showing that:
initiation: the property holds in the initial state.
preservation: the property is preserved by all events, that is, given a state satisfying the property, any possible following state also satisfies the property.
These conditions are particularly interesting because one only has to consider a scope of one (resp. two) state for verifying the first (resp. second) condition, rather than considering a whole trace of unbounded length as in the shared_are_accessible assertion shown above.
To be able to check these two conditions, we must first ensure that the initial state and events are not stated as facts, as facts may remove important behaviors. This requires a very small refactoring of the model:
we change the
initfact into a predicate;we also change the
transitionsfact into a predicate;we extract into a
nextpredicate the formula inside the outermostalwaysoftransitions.
pred init {
// Initially there are no files uploaded nor shared
no uploaded
no shared
}
pred next {
(some f : File | upload[f] or delete[f] or restore[f]) or
(some f : File, t : Token | share[f, t]) or
(some t : Token | download[t]) or
empty or
stutter
}
pred traces {
init
always next
}
The traces predicate will be of no use for our verification by induction but it must still be used as a premise in normal temporal assertions to restrict the verification to valid traces. For instance, shared_are_accessible should be rewritten as follows.
assert shared_are_accessible {
traces implies always shared.Token in uploaded - trashed
}
Moreover, fairness constraint fairness_on_empty should also be moved from a fact into a predicate and called when needed in the liveness assertion.
Let us now come back to our verification by induction. First we specify our tentative invariant as a predicate.
pred inv_shared_are_accessible {
shared.Token in uploaded - trashed
}
Then we assert the conditions for initiation and preservation. In the first case, we say that init implies the invariant; in the second case, invariant preservation means that, in every state that satisfies the invariant, if an event happens, then any following state also satisfies the invariant.
assert init_inv_shared_are_accessible {
init implies inv_shared_are_accessible
}
assert pres_inv_shared_are_accessible {
(inv_shared_are_accessible and next) implies
after inv_shared_are_accessible
}
As explained above, an interesting aspect of this verification technique is that we can focus on traces of length 1 for init_inv_shared_are_accessible and 2 for pres_inv_shared_are_accessible (incidentally, it allows us to rely on a bounded solver, if needed).
check init_inv_shared_are_accessible for 10 but 1 steps
check pres_inv_shared_are_accessible for 10 but 2 steps
Checking both these assertions yields no counterexample, thus establishing that the property is indeed an invariant (up to the given scope of files and tokens, of course). Due to the use of the induction principle, such an invariant is called an inductive invariant.
Verifying this inductive invariant took less than a second on a normal computer, more than 100 times faster than the original check! This gain in speed is interesting as it could allow us to consider larger scopes for signatures, thus increasing our confidence in the correctness of the property.
Non-inductive invariants¶
At this point you might ask: why not check all (supposed) invariants using this method?
Before addressing this question, let us remark that we had to refactor our model to apply the induction principle. One may argue that the resulting model, if still readable, is a little convoluted with respect to the original version, in particular because every temporal assertion should be preceded by the traces premise. Admittedly, it might be considered a low price to pay considering the apparent added value.
A more important issue, however, is that not all invariants are inductive. Consider, for example, the alternative inv_shared_are_uploaded property that says that all shared files are uploaded.
pred inv_shared_are_uploaded {
shared.Token in uploaded
}
Obviously, since inv_shared_are_uploaded is a weakened variation of property inv_shared_are_accessible, it is also an invariant of this model, as the command below confirms.
assert shared_are_uploaded {
traces implies always inv_shared_are_uploaded
}
check shared_are_uploaded for 10 but 1.. steps
But if we proceed to check that inv_shared_are_uploaded is an inductive invariant, then command pres_inv_shared_are_uploaded yields a counterexample.
assert init_inv_shared_are_uploaded {
init implies inv_shared_are_uploaded
}
check init_inv_shared_are_uploaded for 10 but 1 steps
assert pres_inv_shared_are_uploaded {
(inv_shared_are_uploaded and next) implies
after inv_shared_are_uploaded
}
check pres_inv_shared_are_uploaded for 10 but 2 steps
For the sake of readability, we replay the command but with a scope of 1, which also yields a (smaller) counterexample.
check pres_inv_shared_are_uploaded for 1 but 2 steps
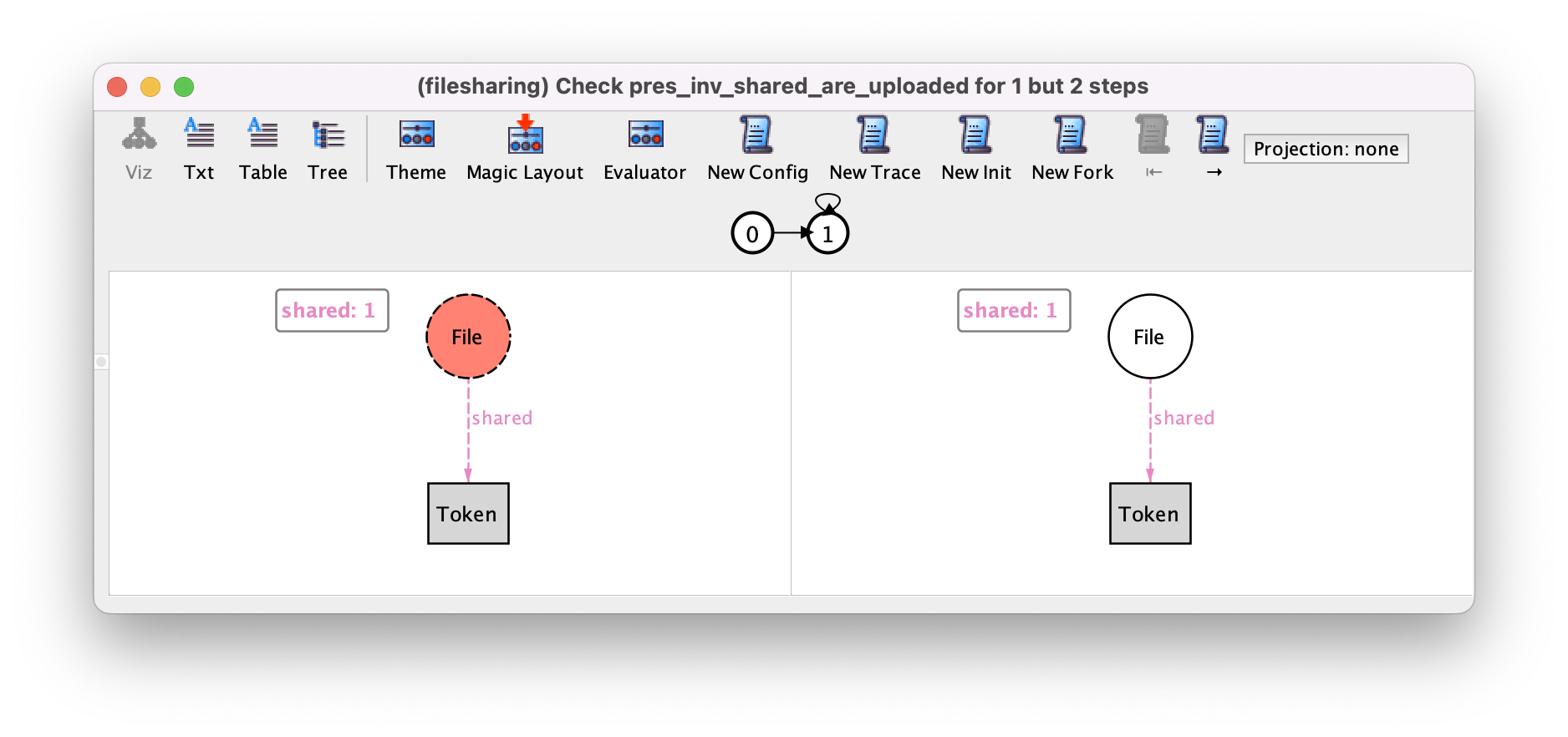
In this counterexample, there is a shared file in the trash in the first states, which is then no longer uploaded after the trash is emptied. The first state satisfies pres_inv_shared_are_uploaded and the second one does not. It might seem contradictory, as we already know that inv_shared_are_uploaded is an invariant. But, after close inspection, it actually appears that these two states are unreachable, that is they do not exist in any possible valid trace: once a file is deleted, it can no longer be shared. This could be confirmed by writing an adequate run command. However, this is in general a bad idea as the command would run for a long time, (because of the absence of a satisfying instance), thus defeating the purpose of using this inductive approach.
What this example illustrates is that this method of verification does not only consider states appearing in all possible traces but also any other state that satisfies the tentative inductive invariant and that has a successor through next. This is why getting a counterexample when checking pres_inv_shared_are_uploaded does not contradict the fact that inv_shared_are_uploaded is an invariant of our model: the former property concerns states related by the next predicate (even unreachable ones), while the latter only concerns reachable states according to traces.
Invariant strengthening¶
Although inv_shared_are_uploaded is not inductive, it does not mean that we cannot rely on the inductive invariant method and can only resort to checking the temporal constraint shared_are_uploaded. Alternatively, a way to check that an invariant such as inv_shared_are_uploaded holds is to exhibit another invariant that is inductive and that is stronger than the former (that is, it implies it). Indeed, since the stronger invariant is inductive, it holds in every reachable state, and since it implies the original invariant, the latter also necessarily holds in every reachable state.
In our case, we already have an invariant known to be inductive at our disposal: inv_shared_are_accessible. We are therefore only left with confirming that it is stronger than inv_shared_are_uploaded:
assert accessible_is_uploaded {
inv_shared_are_accessible implies inv_shared_are_uploaded
}
check accessible_is_uploaded for 10 but 1 steps
This obviously succeeds. However, in general, finding inductive invariants is notoriously hard. For this reason, although it might be less efficient, using a temporal constraint such as shared_are_accessible to check an invariant is a relevant approach, at least as a first step.