Higher-arity relations¶
In the main chapter we’ve seen how to introduce unary relations (as signatures) and binary relations (as fields), and how to compose them in relational expressions. However, Alloy actually supports relations of arity higher than 2: they are simply seen as a set of tuples of a certain arity. We call a relation with arity n > 0 an n-ary relation, and it must be uniform (i.e., all tuples in it must have arity n). Sets and binary relations are 1-ary and 2-ary relations, respectively. Most of Alloy’s relational operators actually apply to relations of arbitrary arity (except for a few that only apply to binary relations). This chapter explores relations with arity higher than 2, which we denote as higher-arity relations to distinguish from sets and binary relations.
Declaring higher-arity fields¶
Let us get back to the file system example from the
Structural modeling chapter, where the content of a directory is specified by a
set of entries that assign a name to each of its objects. Using only binary fields, the
solution we implemented used a signature Entry to register exactly one
name and one object; then a field entries assigned a set of
Entry atoms to each directory. These entries are not really an essential
part of the design of the file system and are not the target of any of the
expected properties, but were required to group names and objects in a single
entity.
An alternative to this approach would be to store the objects and names contained in a directory directly, without creating the auxiliary
Entry signature. In practice, this entails removing the Entry signature and the entries field, and instead create a ternary field
relating directories, names, and objects. In Alloy, such a field could be simply
declared as follows:
sig Dir extends Object {
contents : Name -> Object
}
The range type expression in the declaration of contents is now the Cartesian product of Name and Object, meaning each
directory is assigned a arbitrary set of pairs each with a name and object inside that
directory. Field contents itself is a ternary relation that is a subset of the Cartesian product
Dir -> Name -> Object. A ternary field is simply a set of flatted triples, and likewise binary relations can be navigated in
both directions.
In theory, we can declare fields of an arbitrary arity in an
Alloy model. In practice, relations with a large arity become impossible to
processed by the Analyzer. This limit depends on the size of the universe of
discourse. For instance, a 5-ary field can only be represented in universes with
less than 74 atoms. However, in our experience, relations with arity higher than
3 are very rarely useful, as manipulating them in constraints becomes very cumbersome.
It should also be noted that higher-arity relations can sometimes help
reduce of the size of the universe. In our example, by avoiding
the creation of auxiliary signature Entry we removed all those atoms
from the universe.
Visualizing higher-arity fields¶
Let us for now ignore all additional facts that we had defined for the file
system model (which we will need to adapt to the new ternary field), and just
run the empty example command. We need to remove any scope assigned
to Entry since that signature no longer exists. We will get instances
such as the following.
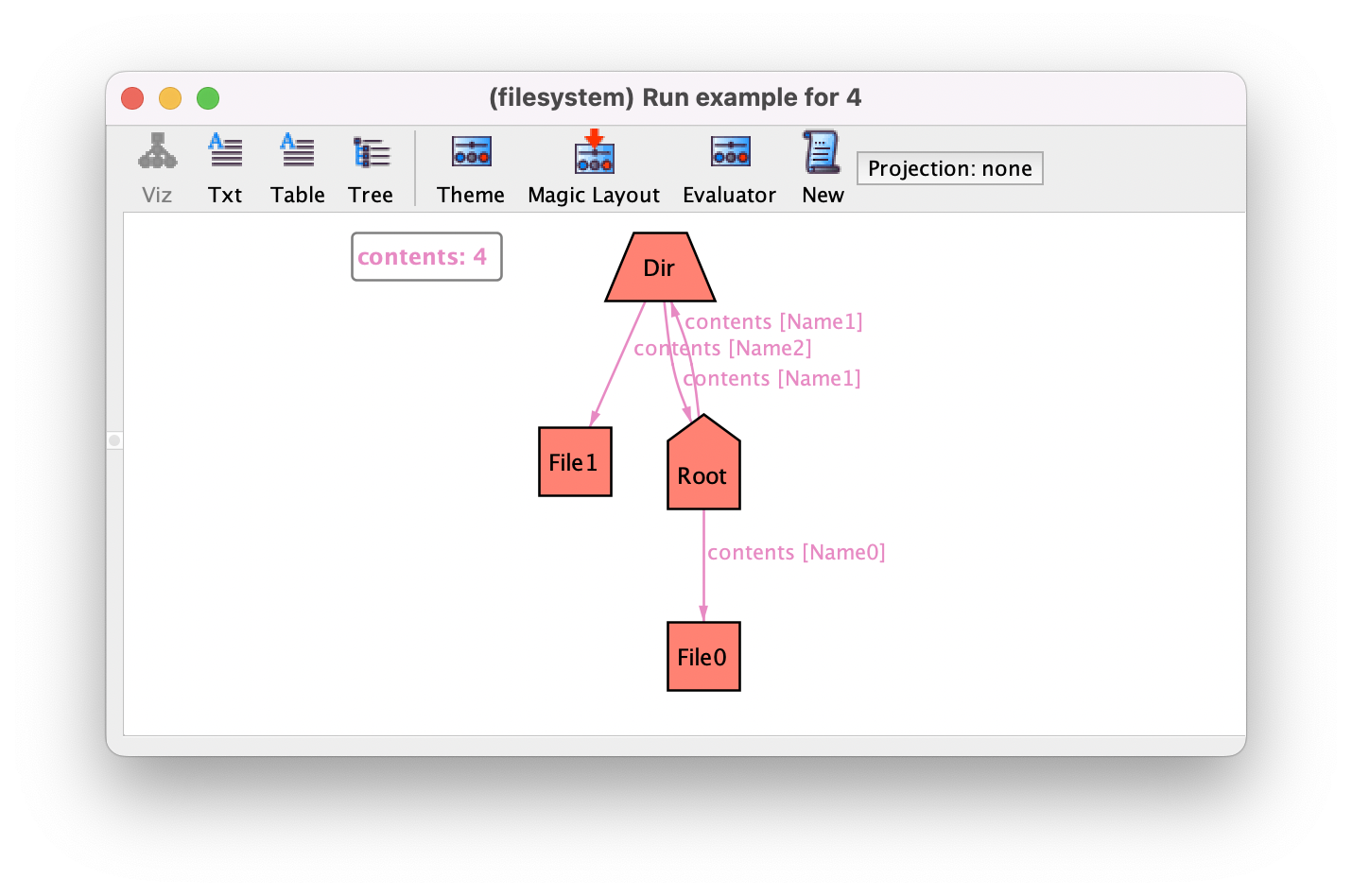
Notice how ternary relations are still represented as edges in the Analyzer’s
visualizer, namely edges between the first and the last in each tuple; the middle
atom is shown as a label in the edge. So, in this instance, Root
contains File0 with name Name0 and Dir with
Name1. For fields of arity higher than 3, additional atoms would added to the
labels of the edges separated by commas.
Specifying constraints¶
The instance above exhibits many of the issues that we addressed in the main
chapter. Let us adapt the facts to the new version of the model with a
ternary field. Most relational operators work for higher-arity relations as they
do for binary ones. Set operators such as intersection (&), union
(+), and difference (-) can be applied between two relations of
the same arbitrary arity. Composition also applies to higher arity relations. If
you have a directory d, d.contents is a binary relation within
Name -> Object containing all pairs of names and objects assigned to
d by contents. Likewise, for an object o,
contents.o is a binary relation pairing directories with the names that
object o has inside them.
The first fact in the model, unique_names, forced different entries of a
directory to have distinct names. The original version of this fact calculated
all entries of each directory with a given name, and forced the resulting set to
have at most one value. In the new version, we can follow a similar strategy, as
follows.
fact unique_names {
// Different entries in the same directory must have different names
all d : Dir, n : Name | lone n.(d.contents)
}
If d.contents is a binary relation containing alls pair of names and
objects assigned to d, n.(d.contents) is a unary relation with
the objects assigned name n in directory d. Since we want at
most one object with each name in a directory, we restrict this set to have
cardinality lone. Parenthesis are needed here because composition
associates to the left and n.d is not a valid expression (it would have
arity 0).
Interestingly, once we encode the content of a directory as a ternary relation,
we can actually enforce this constraint directly when declaring the field.
Higher-arity fields can also be restricted by multiplicity constraints in their
declaration. In this case, we want to enforce that for any directory, and for
any name, there is at most one object related by contents. This could be
enforced as follows, as an alternative to fact unique_names.
sig Dir extends Object {
contents : Name -> lone Object
}
The second fact, no_shared_dirs, forced every directory to appear at
most in one entry. This one can be trivially adapted to the ternary field as
follows. Relation contents.d is a binary relation that pairs all directories that contain d with the respective names. Since a directory can only be contained in a single
directory we should restrict the cardinality of his expression with
lone.
fact no_shared_dirs {
// A directory cannot be contained in more than one entry
all d : Dir | lone contents.d
}
Fact no_dangling_objects forced all objects, except the root, to be
contained in some entry. In the previous version, expression
Entry.object denoted every object referred by any entry. In the ternary
version, we must retrieve all objects related to any object by any name, which
is represented by expression Name.(Object.contents). Given this expression,
the fact could be trivially adapted as follows.
fact no_dangling_objects {
// Every object except the root is contained somewhere
Name.(Object.contents) = Object - Root
}
Fact one_directory_per_entry is no longer needed in this version of the model because we no longer have entries.
Defining relations by comprehension¶
All the facts we have adapted thus far were as complex to specify with the ternary field as
they were with the auxiliary signature Entry and the binary entries field.
Unfortunately, that is not always the case, and the last remaining fact,
no_indirect_containment, is a bit tricky to encode with the ternary
contents field. That fact, through function descendants, relied on
the transitive closure of the binary relation entries.object to collect
all objects indirectly contained in a directory. However, when two ternary
relations are composed, the result is actually a quaternary relation. For
instance, with the ternary contents, contents.contents is a
quaternary relation contained in Dir -> Name -> Name -> Object. So the
transitive closure operations are not well-defined for non-binary relations, and
are forbidden in Alloy.
By inspecting function descendants, it is obvious that the name of the
objects inside a directory is irrelevant to calculate this relation, so what we
need is to convert ternary field contents in Dir -> Name ->
Object to a binary version in Dir -> Object that relates directories
with their content disregarding the name. Unfortunately, there is no
straightforward way to achieve this using only relational operators, and we need
to rely on defining this relation by comprehension.
Relations can be defined by comprehension by quantifying over a sequence of variables,
and keeping only the tuples that satisfy a formula defined over those variables. All relational
operators (except closures) can be rewritten using a relation by comprehension.
For instance, expression Object - Root above could be rewritten as
{ o : Object | o not in Root }, and Dir + File as { o :
Object | o in Dir or o in File }.
For our example, we want to take all directories and objects such that they are
related by some name in contents. This can be specified as a
binary relation defined by comprehension that “selects all
directories d and objects o such that d is related to
o through some atom”. Let us define a new auxiliary function objects
that provides this derived relation.
fun objects : Dir -> Object {
{ d : Dir, o : Object | some d.contents.o }
}
Equipped with this relation, it is now trivial to adapt function
descendants (and consequently, fact no_indirect_containment)
to the ternary field as follows.
fun descendants [o : Object] : set Object {
o.^objects
}
Manipulating ternary relations can become cumbersome, so the Analyzer actually provides an utility module util/ternary that defines functions to project and flip ternary relations. The one we just defined, that retrieves the first and last columns of a ternary relation, is provided by function select13.
If we now run the empty example command once again, we will get
instances such as the following, where the issues seem to have been fixed.
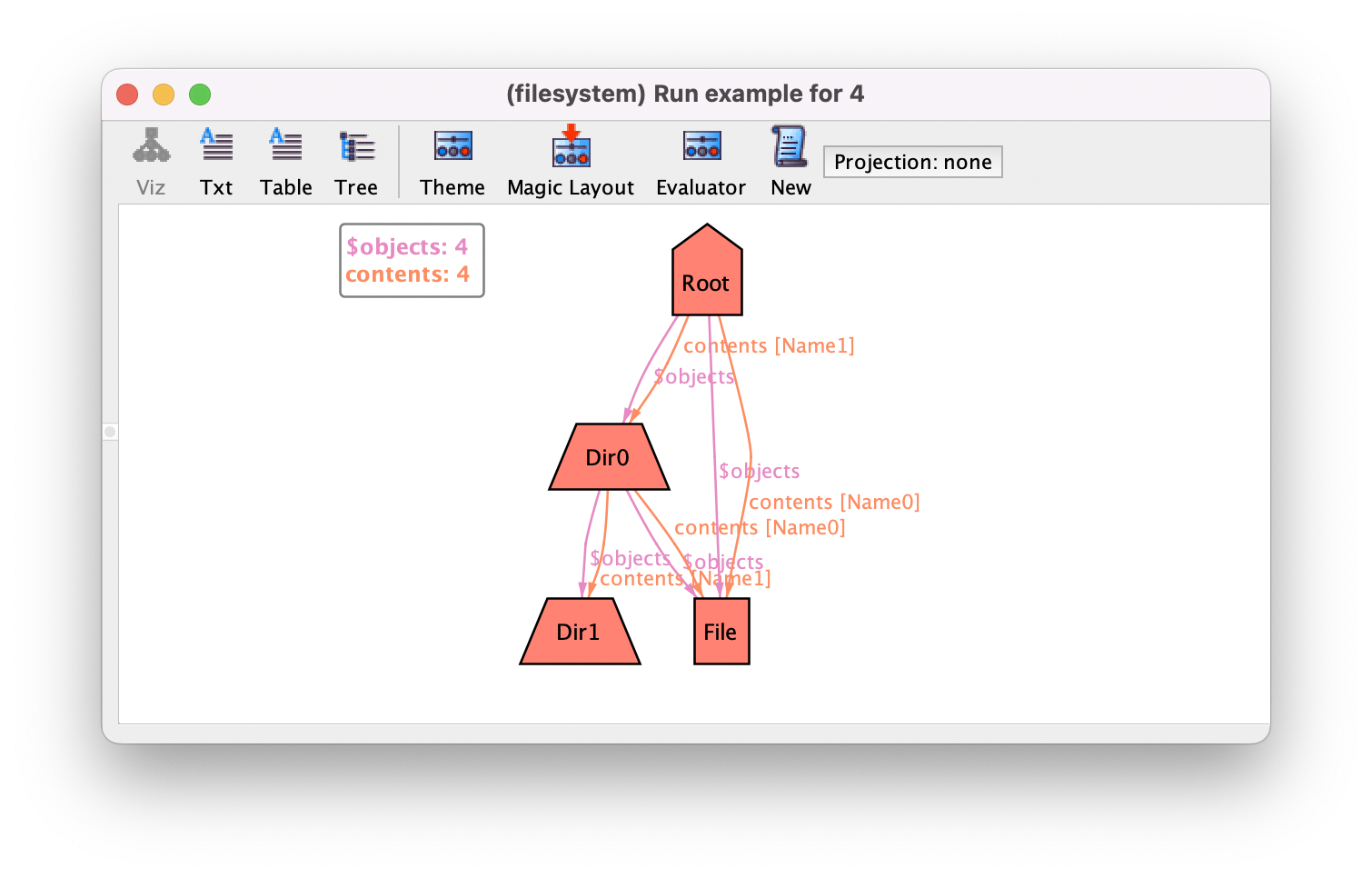
You’ll notice that there is now a new element in the visualization, the value of
function objects prefixed by a $. Alloy introduces all
functions without parameters in the visualization, and in one of the advanced topics we show how these can be used to improve the visualization of instances. For now we can just
hide it as any other relation by choosing Off in the Show
as arcs theme option for objects. This will result in the following
cleaner instance.
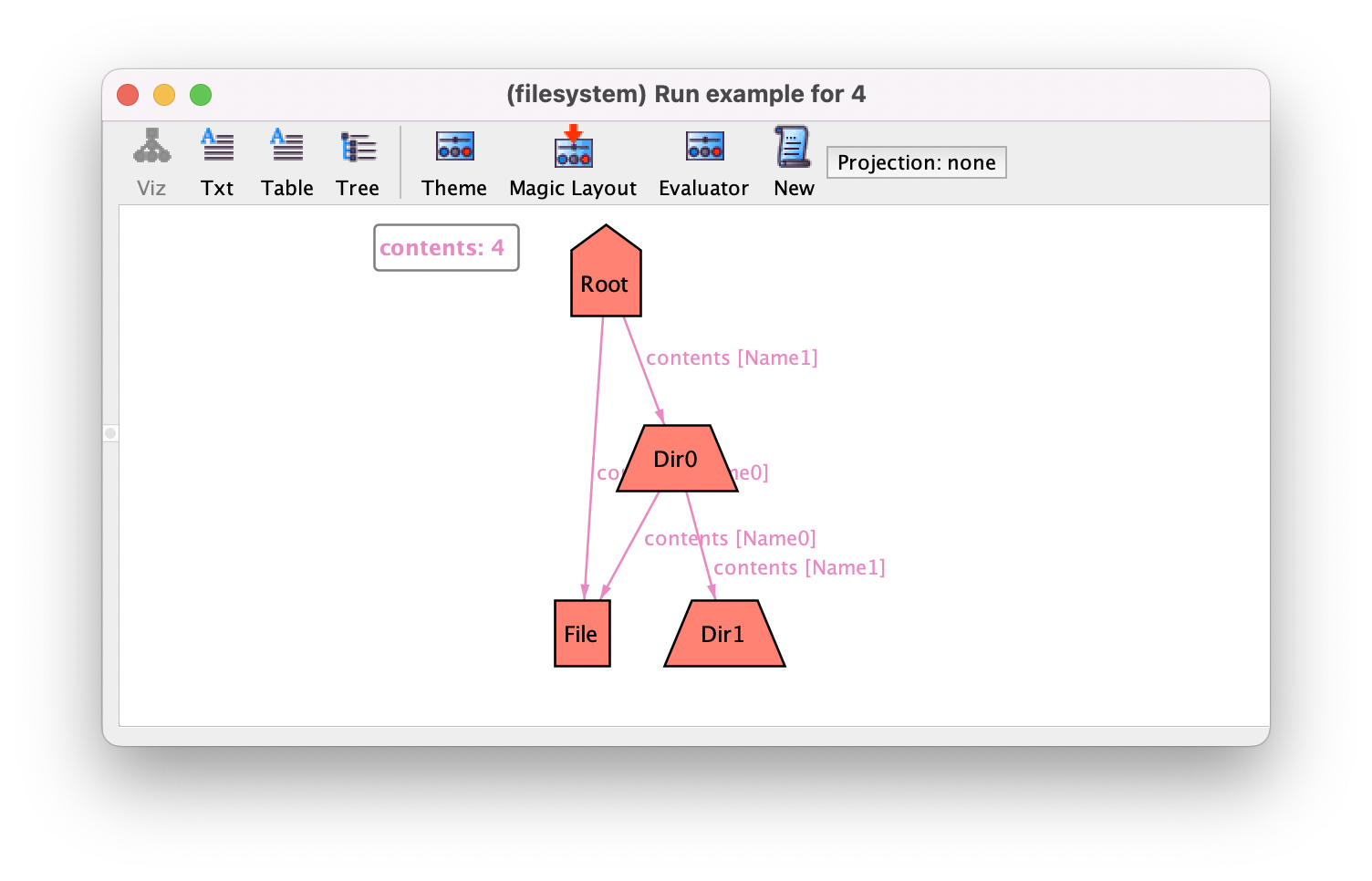
To finish we should of course check the
no_partitions assertion. Given that no_partitions was defined by calling function descendants (through predicate reachable), nothing
needs to be adapted in this assertion. After executing the
command, the Analyzer will report no counter-examples, as expected.
As a last note, it’s not always evident when higher-arity relations should be used in a model. There is a sweet spot where employing a few higher-arity relations (almost always, ternary relations) improves the readability and maintainability of our specifications, while also improving the performance of the Analyzer by reducing the number of signatures and fields in a model (and thus the number of atoms and free relations to be solved). If too many higher arity relations are used (or relations of too high arity), models can become unmanageable and they can also have a negative impact on performance (since expressions can become considerably more complex).